.jpg)
このブログの名前は? そう、赤本ブログ!
赤本といえば、やっぱり「過去問」ですよね。
夏も終わり、そろそろ過去問演習を始めた、または始めようと思っているものの何をどう使えばいいのかわからない、という人も多いのではないでしょうか。
そこで今回は、数学の過去問の使い方について、みなさんの疑問にお答えいたします!
|
目次
Q5 数学の苦手な人が、過去問を解くときに注意しなければならない点は何ですか?
|
| Q1 |
そもそも過去問は何のために解くものですか? |
過去問を解くのは目標と現状の分析のためです。これは第1回でも少し取り上げましたね。決して、同じ問題が出るかもしれないから、ではありません。
陸上競技の100m走で考えてみましょう。
記録を出すためには、がむしゃらに何度も走りさえすればいいわけではなく、フォームを動画で撮ったり、人に見てもらったりして分析した上で、実際に体を動かしながら、こうしてみよう、ああしてみよう、と練習するでしょう。
どんな競技にも同じようなことが言えると思いますが、これはスポーツだけでなく勉強でも同じです。過去問とそれを解いたものは、目標と自分の現状を知るための貴重な資料です。それを分析せず闇雲に勉強するのは、がむしゃらに何度も走るだけの練習と同じです。
| Q2 |
いつから始めればいいですか? |
「(第2回でお話ししたような)基礎のインプットが7割方できている」かつ「過去問の解答・解説を読んでさっぱりわからないレベルではない」状態であれば、そろそろ過去問を始めるタイミング。多くの受験生にとっては、ちょうど今(9~10月頃)ではないでしょうか。
| Q3 |
何年分やればいいですか? |
年数はできるだけたくさん解くに越したことはありません。ただ、量をやるだけやって復習が追いつかなかったり、新しい年度のものを直前期に残すためにめちゃくちゃ古い年度から始めたら結局新しいものを解けずに終わってしまったり…といったよくあるダメなパターンにならないようにしましょう。
自分が無理なくこなせる量を判断するのは難しいですが、量を稼ごうと思っても、中途半端に終わってしまっては元も子もない、ということを心に留めておきましょう。
多くの受験生は、数学だけでなく、英語や国語などの他教科も勉強しなければなりませんし、数学の勉強も過去問だけやっていればいいわけではありません。
ですから、他教科を含めて総合的に計画を立て、クオリティを担保できる範囲で、やりきれそうな分だけやりましょう。
また、1年分だけやっても傾向が読み取れないので、新しい年度のものを最低でも2、3年分はやりましょう。
| Q4 |
どのように使えばいいですか? |
何をどれだけ勉強すれば効果的なのか、それは人それぞれです。ここでは、あなた自身が自分に必要なものを判断できるよう、3つの方法を伝授します。以下の①から③の方法を適宜組合せて、自分に合ったやり方を探しながら進めていくとよいでしょう。
|
① 年度ごとに、本番と同じ制限時間で解く 制限時間に対して問題の量や計算量がどれぐらいか、自分がどこまで解けたのかをチェックしましょう。記述式の場合、制限時間には答案作成の時間も含まれていることに注意してくださいね。また大問ごとにかかった時間や反省点も記録しておくと、次に活かしやすくなると思います。
② 時間無制限で解き、解答を確認する 解けなかった問題について、何があれば解けたのかを考えましょう。①で解けなかったのに②で解けたのなら、足りなかったのは時間。しかし時間をかけてもダメなら、足りないのは知識か、それとも発想か、ということになります。 解けなかった原因が時間であれば、どこで余計な時間を使ったのかを調べ、計算の工夫などを考える。知識であれば、すぐに調べて覚えなおす。発想であれば、その分野の演習(アウトプット)を増やす。その他にも具体的な対策を考えて実行しましょう。
③ 分野別に解く たくさんの年度の過去問が手に入る大学であれば、例えば確率の問題ばかりを集中していくつか解くなど、ひとつの分野にまとめて取り組んでみると、問われ方や重視されている考え方が見えてくることが多いです。
|
いずれも大事なことは、「過去問は分析・復習を次に活かしてなんぼ」ということです。反省点や気づいたことは、すぐに見られるようノートなどにまとめておきましょう。
| Q5 |
数学の苦手な人が、過去問を解くときに注意しなければならない点は何ですか? |
解答を見るときに気をつけてほしいのが、「解答と思考の順番は必ずしも一致しない」ということです。次の例題を見てみましょう。
|
例題 |
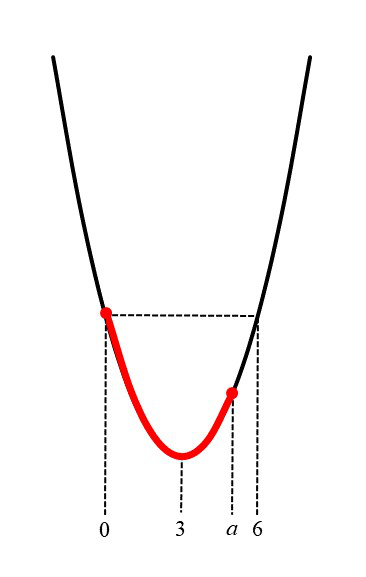
a > 0 を定数とする。f (x) = x2 − 6x + 2 の 0 ≦ x ≦ a における最大値 M を求めよ。 |
|
解答 f (x) = (x−3)2 − 7 より (i) 0 < a < 6 のとき M = f (0) = 2
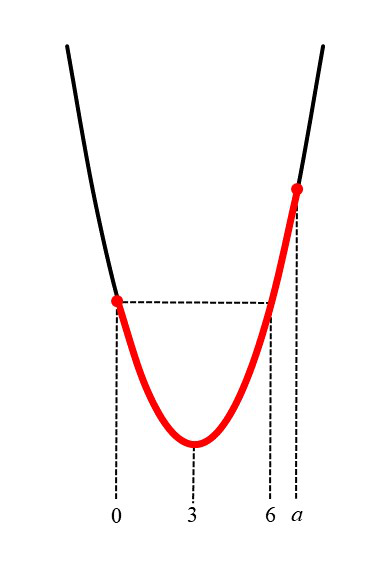
(ii) a ≧6 のとき
M = f (a) = a2 − 6a + 2
|
ここで解答は、以下の流れになっています。
|
aの範囲 ↓ グラフ ↓ 最大値 |
しかし実際に問題を解くときには、次のようなルートで考えているのではないでしょうか。
|
グラフをかく ↓ aを動かして最大値がどう変化するかをみる ↓ 場合分けをするaの範囲を決める |
この問題を初めて解こうとした人は、解答をひと目見て、「突然場合分けが始まった!なぜ、最初からどう分ければいいのかがわかるのだろう?」と感じるかもしれません。
でも、そうではないですよね。
別のところにグラフを書いてみて、いろんな状況を考えた結果、場合分けすべきだということ、そしてどう場合分けすればいいかが判明するので、aの範囲ごとにグラフを書き直して解答としているのです。
もちろん簡単な例なので、ここまで意識せずに解ける人も多いかもしれませんが、難しい問題であっても同じことがよくあります。
問題集などを使って勉強をするときには、このように「なぜ思いついたのだろう」「実際の思考はどういう流れなのだろう」といったことまで探りながら解答を読めば、新しい問題に自力で対処する力が少しずつついてくると思います。
また、数学が苦手な人にありがちなのですが、特に演習問題を解く際(アウトプット)に、問題を見て「解き方がわからない」からといって、すぐ何かを参照したり、解答を見たりするのはやめましょう。解答の方針まで至らなかったとしても、まずは与えられた条件を言い換えてみたり図で表したりしながら、できる限り思考を進める、というのも、自分で考える力を養うためには重要なことです。分析は大切ですが、それだけでもだめで、実際に全力で走る練習を重ねることも必要だということですね。
|
★ポイント★
|
◎ 最後に、今勉強を頑張っている受験生へ、応援メッセージをお願いします |
空っぽの箱に荒い知識をどんどん取り込んでいく期間(インプット)が終わった今、これまで以上に、目標と現状を分析し、何が足りていないのかを細かく探りながら勉強していくことが大切になってきます。
つまり、自分は何ができないのかに着目せざるを得ないわけですが、自分の「できない」と向き合うのが辛いと感じる人もいるかもしれません。
でも、それが勉強するということなんです。
しっかり向き合った人ほど着実に成果は出ます。自分の「できない」に目を瞑ったまま、なんとなく勉強を続けるのか。しんどいこともあるかもしれないけれど、合格を勝ち取るために己と向き合っていくのか。今一度、方針を考えてみてください。
ただ、辛くなってきたときに勘違いしてほしくないのは、「できないことがある」ということが、「あなたがダメな人間である」ということではない、ということです。
冷静に分析をしながら、ときには「これまでやってきたこと、できたこと」も確認して励みにしつつ、辛抱強く挑み続けていってください。

住吉千波(すみよし・ちなみ)
河合塾講師、東進ハイスクール・東進衛星予備校講師などとして高校生や大学受験生に、個人では小学生から大人まで、幅広い層に数学を教えている。京都生まれ京都育ち。神戸大学大学院理学研究科数学専攻修了。河合文化教育研究所研究員。
| 連載予定 |
| 第1回『受験数学の始め方』(2021年4月2日にアップ済み) |
| 第2回『夏休みの過ごし方』(2021年6月21日にアップ済み) |
| 第4回『共通テストへの備え方』(2021年12月1日にアップ済み) |
| 第5回『2次試験への備え方』(2022年1月17日にアップ済み) |
お楽しみに!
関連商品
|
|
赤本ノート/赤本ルーズリーフ 過去問を解きながら志望校の「傾向」を分析し、自分だけの「対策」を練ることができる学習ノート&ルーズリーフ!フォームを埋めるだけで、自己分析や苦手発見ができます! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|