.jpg)
「なんか、数学って苦手だなあ」
こんなもやもやした思いを抱えたまま受験生になった人はいませんか? 一度苦手意識を持ってしまうと、解消するのは難しいですよね。
そんな悩める受験生にお届けするのがこの連載企画、『苦手な人のための受験数学』です。予備校講師としてこれまで様々な生徒に数学を教えてこられた住吉千波先生に、効果的な勉強法を全5回にわたってお聞きします。
今回は第1回「受験数学の始め方」です。これを読んで、受験生活を気持ち良くスタートしましょう!
|
目次
Q2 ではスタートとゴールを確認するために、具体的に何をすればよいでしょうか?
|
Q1 |
受験生が受験対策として最初にやるべきことは何ですか? |
4月になり、いよいよ受験学年がスタート。気持ち新たに意気込んでいる人も多いのではないでしょうか。
さて、今は「あれをやるぞ、これもやるぞ」と、たくさんのやりたいことや計画があると思いますが、スタートとゴールは見えていますか?
当たり前ですが、スタート(今の学力)とゴール(志望校)は人によって違います。何をどれだけ勉強しなければならないかは人それぞれです。だから、意外と忘れられがちではあるのですが、まずは自分のスタートとゴールを確認してから、受験勉強を始めてほしいのです。
Q2 |
ではスタートとゴールを確認するために、具体的に何をすればよいでしょうか? |
そのためにはまず、志望校の過去問を1年分だけ解いてみるのがいいと思います。
過去問と聞いて、「まだそんなレベルじゃない」とか「解けるわけない」とか、あるいは「直前にとっておきたい」と思った人がいるかもしれません。でも、そのレベルに届いていなくても、全く解けなくてもいいんです。目的はあくまでも自分の実力を確認すること。「全く解けないことが確認できた」「解けないと思っていたけど、小問集合は解けた」など、入試直前の冬にできるようになりたい問題のレベルに対して、今の自分がどこまで対応できるのかを、まずは確認しましょう。
それと同時に、これから何をしなければならないのか、勉強の進め方や目標を考える目安になります。「冬にはこのレベルの問題に対応できる力が必要なんだ」「問題の雰囲気はこんな感じなんだ」ということがわかり、これから何を目指して勉強すればよいのか、がはっきりすると思います。
できれば、問題を解くときに解答時間も確認しておくとよいでしょう。もちろん現段階では、解答時間内に解けなくても大丈夫です。しかし、「スピードも要求される」とか「難しいけど1問にじっくり時間がかけられる」など、その大学の入試数学の性格がよりリアルに見えてくるので、解答時間に注意して過去問を解いてみるとよいと思います。
このように過去問を使ってスタートとゴールの距離感をつかむことで、途中でクリアしなければならないことが見えてくるはずです。
Q3 |
公式や定理はどのように覚えたらよいですか? |
もしかしたら志望校の問題を解きながら「出題されたことのある公式や定理はカンペキに覚えなきゃ…」と考えた人がいるかもしれません。もちろん、公式は覚えるに越したことはありませんが、基本的に数学の試験では、覚えたことをそのまま書けばいい、なんて問題は出ません。
公式や定理を形式的に覚えるのではなく、「なぜそれが成り立つのか」「どういう場面で用いることができるのか」というところまで学び、自分のものにしましょう。そこまでして初めて、使える道具になるのです。
たとえば、高校1年生で習う「反復試行の確率」の公式を考えてみましょう。
反復試行の確率1回の試行で事象Aの起こる確率がpであるとする。 その試行をn回繰り返したとき、事象Aがちょうどr回起こる確率は nCrpr(1 − p)n−r |
これを,少なくとも「1 カイノ シコウデ ジショウ A ノ・・・」とでも覚えてさえいれば,
|
例1 |
さいころを5連続で振るとき、3の倍数の目がちょうど2回出る確率を求めよ。 |
という問題に対しては、公式のpやnを問題文からそれぞれ当てはめていけばいいので
|
|
と答えを導くことができると思います。
ただ、これが次のような形で出題されたらどうでしょうか。
|
例2 |
赤球が2個、白球が3個、青球が4個入っている箱から1つ球を取り出し、色を確認したあと、箱に戻すという試行を5回行うとき、赤球が2回、白球が1回、青球が2回出る確率を求めよ。
|
覚えただけの公式に当てはめようとすると、n は n = 5 とできそうですが、r と p の意味がわかりませんよね。このように、公式を丸暗記しただけでは、少し問われ方が違っただけで対応できなくなってしまいます。
そもそも、最初に挙げた「反復試行の確率」の公式の意味は、「例1」を通して考えると次のようになります。

|
さて、今の考え方がわかれば、「例2」の解き方もほとんど一緒です。覚えた公式の意味がしっかりわかって初めて、試験で使える実用的な道具になります。いや、もはや、この考え方が自分のものになっていれば、公式は覚えようとする前にすでに身についてしまっているかもしれませんね。
|
|
ここで挙げたのはシンプルな例ですが、他の公式や定理、典型問題の解法などにも、同じことが言えます。基本的に入試に「そのまま」は出てきません。少なからず、「その場の状況に応じて、自分で」対処する必要があります。そのために、まずは形だけでない、しっかりとした土台を築いてください。それは決して容易なことではありませんし、「基礎」を積み上げる作業は地味で、もどかしく感じることがあるかもしれません。しかし、ここを頑丈にしておけば、それだけでかなりの力がつきます。
もちろん、入試で公式や定理の証明自体が問われることもありますので、基礎を意識した勉強をしていれば一石二鳥ですね。
|
★ポイント★
|

住吉千波(すみよし・ちなみ)
河合塾講師、東進ハイスクール・東進衛星予備校講師(過去問・模試解説担当)として高校生や大学受験生に、個人では小学生から大人まで、幅広い層に数学を教えている。京都生まれ京都育ち。神戸大学大学院理学研究科数学専攻修了。河合文化教育研究所研究員。
| 連載予定 |
| 第2回 『夏休みの過ごし方』 (2021年7月2日にアップ済み) |
| 第3回 『過去問の使い方』 (2021年10月15日にアップ済み) |
| 第4回 『共通テストへの備え方』 (2021年12月1日にアップ済み) |
| 第5回 『2次試験への備え方』 (2022年1月17日にアップ済み) |
お楽しみに!
関連ページ
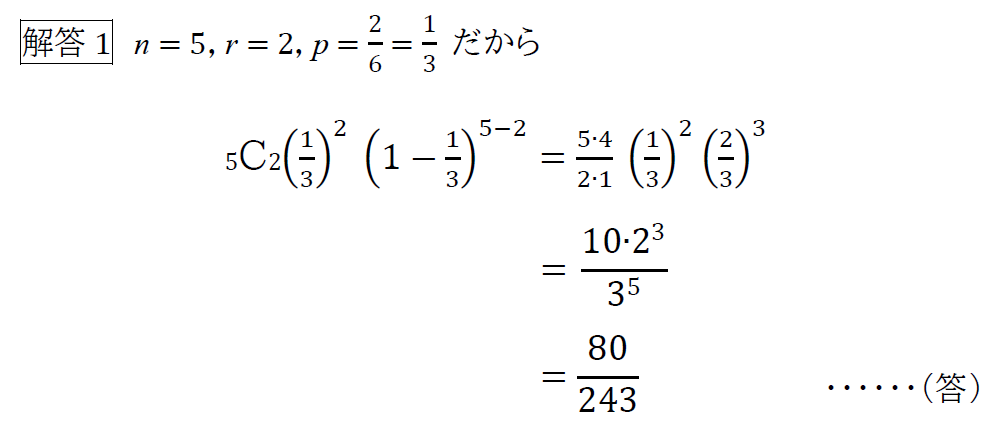
.png)





























